Polarizazioa antenen oinarrizko ezaugarrietako bat da. Lehenik eta behin, uhin lauen polarizazioa ulertu behar dugu. Ondoren, antenen polarizazio mota nagusiak aztertu ditzakegu.
polarizazio lineala
Uhin elektromagnetiko plano baten polarizazioa ulertzen hasiko gara.
Uhin elektromagnetiko planar batek (EM) hainbat ezaugarri ditu. Lehenengoa, potentzia norabide bakarrean bidaiatzen duela da (ez da eremurik aldatzen bi norabide ortogonaletan). Bigarrena, eremu elektrikoa eta eremu magnetikoa elkarren perpendikularrak dira eta elkarren ortogonalak. Eremu elektrikoak eta magnetikoak uhin lauen hedapen-norabidearekiko perpendikularrak dira. Adibide gisa, (1) ekuazioak emandako maiztasun bakarreko eremu elektriko bat (E eremua) kontsidera dezagun. Eremu elektromagnetikoa +z norabidean bidaiatzen ari da. Eremu elektrikoa +x norabidean zuzenduta dago. Eremu magnetikoa +y norabidean dago.
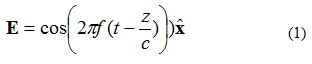
(1) ekuazioan, behatu notazioa: . Hau bektore unitario bat da (luzera duen bektorea), eta horrek adierazten du eremu elektrikoaren puntua x norabidean dagoela. Uhin laua 1. irudian ageri da.
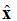
1. irudia. +z norabidean bidaiatzen duen eremu elektrikoaren irudikapen grafikoa.
Polarizazioa eremu elektriko baten traza eta hedapen-forma (kontura) da. Adibide gisa, kontsidera dezagun uhin lauen eremu elektrikoaren ekuazioa (1). Eremu elektrikoa (X,Y,Z) = (0,0,0) den posizioa denboraren funtzio gisa ikusiko dugu. Eremu honen anplitudea 2. irudian irudikatzen da, denboran hainbat unetan. Eremua "F" maiztasunean oszilatzen ari da.
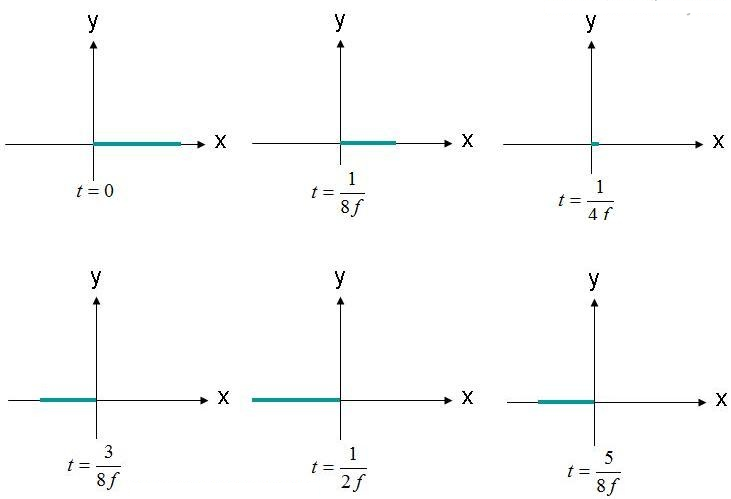
2. irudia. Behatu (X, Y, Z) = (0,0,0) eremu elektrikoa denbora ezberdinetan.
Eremu elektrikoa jatorrian ikusten da, anplitudean aurrera eta atzera oszilatzen. Eremu elektrikoa beti adierazitako x ardatzean zehar doa. Eremu elektrikoa lerro bakar batean zehar mantentzen denez, eremu hau linealki polarizatuta dagoela esan daiteke. Gainera, X ardatza lurrarekiko paraleloa bada, eremu hau horizontalki polarizatuta dagoela ere deskribatzen da. Eremua Y ardatzean zehar orientatuta badago, uhina bertikalki polarizatuta dagoela esan daiteke.
Linealki polarizatutako uhinek ez dute zertan ardatz horizontal edo bertikal batean zehar zuzendu. Adibidez, 3. irudian erakusten den lerro batean zehar muga bat duen eremu elektriko uhin bat ere linealki polarizatuta egongo litzateke.
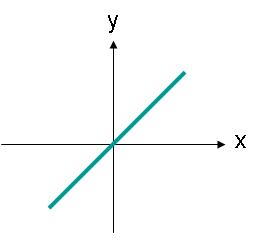
3. irudia. Angelu bat den ibilbidea duen uhin linealki polarizatuaren eremu elektrikoaren anplitudea.
3. irudiko eremu elektrikoa (2) ekuazioaren bidez deskriba daiteke. Orain, eremu elektrikoak x eta y osagaiak ditu. Bi osagaiak tamaina berekoak dira.
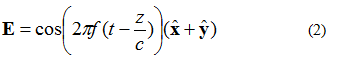
(2) ekuazioari buruz kontuan hartu beharreko gauza bat bigarren faseko xy osagaia eta eremu elektronikoak dira. Horrek esan nahi du bi osagaiek anplitude bera dutela uneoro.
polarizazio zirkularra
Orain, demagun uhin lau baten eremu elektrikoa (3) ekuazioak ematen duela:
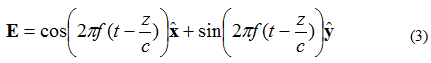
Kasu honetan, X eta Y elementuak 90 graduko desfasean daude. Eremua (X, Y, Z) = (0,0,0) bezala ikusten bada berriro ere lehen bezala, eremu elektrikoaren denboraren araberako kurba 4. irudian erakusten den bezala agertuko da.
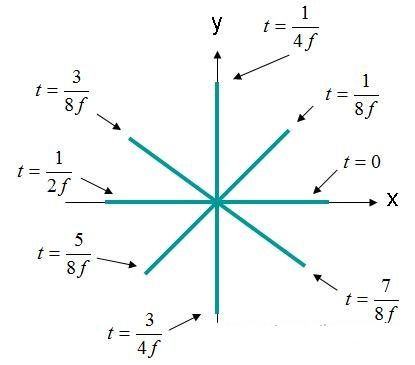
4. irudia. Eremu elektrikoaren indarra (X, Y, Z) = (0,0,0) EQ domeinua. (3).
4. irudiko eremu elektrikoak zirkulu batean biratzen du. Eremu mota hau zirkularki polarizatutako uhin gisa deskribatzen da. Polarizazio zirkularraren kasuan, irizpide hauek bete behar dira:
- Polarizazio zirkularraren estandarra
- Eremu elektrikoak bi osagai ortogonal (perpendikular) izan behar ditu.
- Eremu elektrikoaren osagai ortogonalek anplitude berdinak izan behar dituzte.
- Kuadraturako osagaiak 90 graduko desfasean egon behar dira.
4. irudiko uhinaren pantailan bidaiatzen bada, eremuaren errotazioa erlojuaren orratzen kontrako noranzkoan eta eskuineko noranzkoan polarizatuta dagoela esaten da (RHCP). Eremua erlojuaren orratzen noranzkoan biratzen bada, eremua ezkerreko polarizazio zirkularrekoa izango da (LHCP).
Polarizazio eliptikoa
Eremu elektrikoak bi osagai perpendikular baditu, 90 graduko fasetik kanpo baina magnitude berdinekoak, eremua eliptikoki polarizatuta egongo da. +z norabidean bidaiatzen duen uhin lau baten eremu elektrikoa kontuan hartuta, (4) ekuazioak deskribatzen duena:
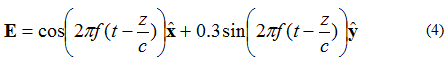
Eremu elektrikoaren bektorearen puntak hartuko duen puntuaren kokapena 5. irudian ematen da.
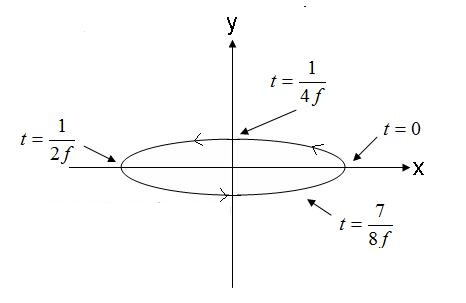
5. irudia. Elipse formako polarizazio-uhinen eremu elektriko bizkorra. (4).
5. irudiko eremua, erlojuaren orratzen kontrako noranzkoan bidaiatzen duena, eskuineko eliptikoa izango litzateke pantailatik kanpo bidaiatzen badu. Eremu elektrikoaren bektorea kontrako noranzkoan biratzen badu, eremua ezkerreko eliptikoki polarizatua izango da.
Gainera, polarizazio eliptikoak bere eszentrikotasunari egiten dio erreferentzia. Eszentrikotasunaren eta ardatz nagusiaren eta txikiaren anplitudearen arteko erlazioa. Adibidez, (4) ekuazioko uhin-eszentrikotasuna 1/0.3 = 3.33 da. Eliptikoki polarizatutako uhinak ardatz nagusiaren norabidearen bidez deskribatzen dira gehiago. (4) uhin-ekuazioak x ardatzaz osatutako ardatz bat du batez ere. Kontuan izan ardatz nagusia edozein plano-angelutan egon daitekeela. Angelua ez da beharrezkoa X, Y edo Z ardatzera egokitzeko. Azkenik, garrantzitsua da kontuan izatea polarizazio zirkularra eta lineala polarizazio eliptikoaren kasu bereziak direla. 1.0 eszentriko eliptikoki polarizatutako uhin bat zirkularki polarizatutako uhin bat da. Eszentrikotasun infinituko uhin eliptikoki polarizatutakoak. Linealki polarizatutako uhinak.
Antena polarizazioa
Orain, uhin plano polarizatuen eremu elektromagnetikoak ezagutzen ditugunez, antena baten polarizazioa modu sinplean definitzen da.
Antenen Polarizazioa Antena baten urruneko eremuaren ebaluazioa, sortzen den erradiazio-eremuaren polarizazioa. Horregatik, antenak askotan "polarizazio linealeko" edo "polarizazio zirkularreko eskuineko antena" gisa sailkatzen dira.
Kontzeptu sinple hau garrantzitsua da antena komunikazioetarako. Lehenik eta behin, horizontalki polarizatutako antena batek ez du komunikatuko bertikalki polarizatutako antena batekin. Elkarrekikotasun teoremaren ondorioz, antenak modu berean transmititzen eta jasotzen du. Beraz, bertikalki polarizatutako antenek bertikalki polarizatutako eremuak transmititzen eta jasotzen dituzte. Beraz, bertikalki polarizatutako eta horizontalki polarizatutako antena bat transmititzen saiatzen bazara, ez da harrerarik izango.
Kasu orokorrean, elkarrekiko angelu batean ( ) biratzen diren bi antena polarizatu linealki badaude, polarizazio-desadostasun honen ondoriozko potentzia-galera polarizazio-galera faktorearen (PLF) bidez deskribatuko da:
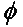
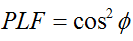
Beraz, bi antenek polarizazio bera badute, haien erradiatzaile elektroi-eremuen arteko angelua zero da eta ez dago potentzia-galerarik polarizazio-desadostasunaren ondorioz. Antena bat bertikalki polarizatuta badago eta bestea horizontalki, angelua 90 gradukoa da, eta ez da potentziarik transferituko.
OHARRA: Telefonoa buruaren gainetik angelu desberdinetara mugitzeak azaltzen du zergatik handitu daitekeen harrera batzuetan. Telefono mugikorren antenak normalean polarizatuta daude linealki, beraz, telefonoa biratzeak telefonoaren polarizazioarekin bat etor dezake askotan, eta horrela harrera hobetzen du.
Polarizazio zirkularra antena askoren ezaugarri desiragarria da. Bi antenak zirkularki polarizatuta daude eta ez dute seinale galerarik jasaten polarizazio desadostasunaren ondorioz. GPS sistemetan erabiltzen diren antenak eskuineko zirkularki polarizatuta daude.
Orain, demagun antena polarizatu linealki polarizatuak uhin polarizatuak jasotzen dituela. Era berean, demagun antena polarizatu zirkularki polarizatu batek uhin polarizatuak linealki jasotzen saiatzen dela. Zein da ondoriozko polarizazio-galera faktorea?
Gogoratu polarizazio zirkularra, egia esan, bi uhin polarizatzaile lineal ortogonal direla, 90 graduko desfasean. Beraz, polarizazio linealeko (LP) antena batek polarizazio zirkularreko (CP) uhinaren fase osagaia bakarrik jasoko du. Beraz, LP antenak 0,5eko (-3dB) polarizazio desadostasun galera izango du. Hori egia da LP antena edozein angelutan biratzen den ere. beraz:
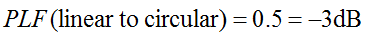
Polarizazio-galera faktorea batzuetan polarizazio-eraginkortasuna, antena-desadostasun faktorea edo antena-harrera faktorea bezala ezagutzen da. Izen horiek guztiek kontzeptu berari egiten diote erreferentzia.
Argitaratze data: 2023ko abenduaren 22a







